
レンタルBCのサイズ判定。
前回はこれを自動化しました。
実際に配ろうとしてみると…
なぜか今日は女性ゲストばかりで、XSのBCが足りない!
本当なら全員XSだけど、Sで行けなくもない人が何人かいるから、そういう人にはSを渡そう…
こんな場面は珍しくないのでは無いでしょうか?
慣れてくると『イイ感じ』に割り当てることが出来るのですが、少し失敗すると、帳尻が合わなくなったり…
ありますよね(笑)
なんとなく配っている様でも、きっと頭の中で色々と考えているわけで、ということはこれすらも自動化出来るのでは!?
今回はそんな試みです。
つまり…
在庫数に応じて多少の誤差を許容しつつ、全体で誤差が最小になる配り方を考える。
ということです。
要は、一部の人がハッピー、一部の人が最悪、ではなく全体的にまぁまぁ、にしましょうということです(笑)
頭の中では何が起きている?
実際のコードに落とし込むにあたり、まずは話を簡略化して考えてみました。
5人にブーツを配ることを想定して、それぞれのサイズの在庫数を定めて…
まずは小さいサイズから。
そのサイズを必要としている人が多すぎる場合には、次に大きいサイズを渡した場合の誤差を見て…
その誤差が大きい人には本来のサイズを渡す。
それを繰り返し…
あっ、これだと小さいサイズが余ってる場合に対応できないから…
挫折しました。
しかし実際に同じような問題は長い人類の歴史の中で生まれていたはずで、絶対に解決する方法があるはず…
とうことで、facebookで助けを求めてみました。
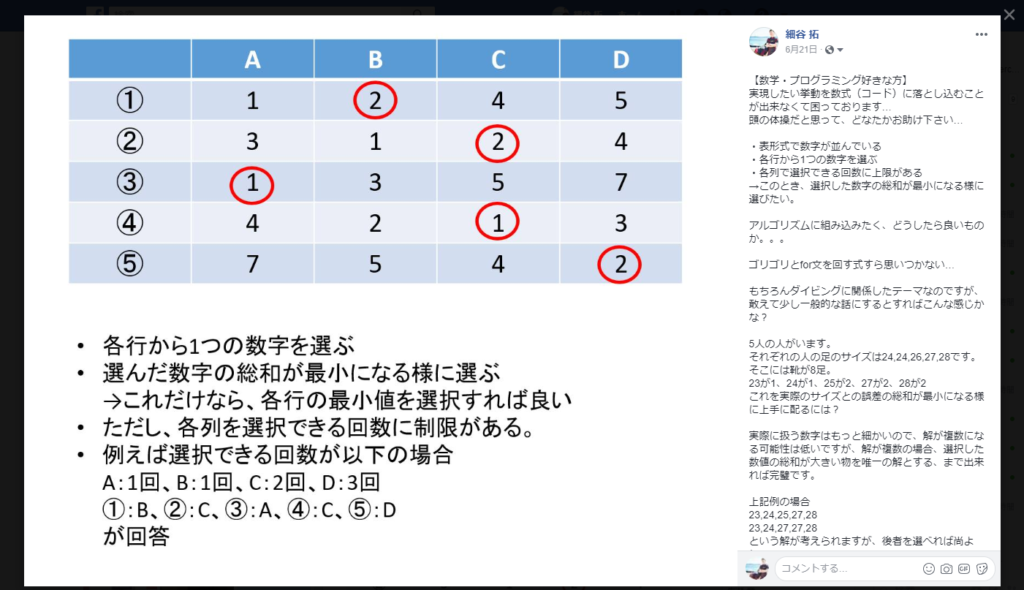
コメントを頂いた方々、ありがとうございました。
しかし、核心を突く答えはえられず…
1人だけ、この問題を解決する糸口を知っていそうな友人が居たので、訪ねてみることにしました。
小学校時代、数学に関して常人離れした頭脳を誇っていたA君。
小学校時代に高校数学を解いていた彼。
その後、高校までは同じ学校でしたが、彼は東大、同大学院と進み現在は京大で助教を務めているとか。
そんな彼からの返答がこちら。
どうやら割り当て問題と言われているらしく、良い方法が色々知られているらしいよ。
東工大のOCWによると、ハンガリー法というのが知られていて比較的簡単そうに見えるね。
ただし、今の問題をちょっと変形する必要があって
- 列の中から複数回選ぶ代わりに、同じ列を加えて、1つの列から1回しか選べないことにする。
- さらに全ての成分が0となるようなダミーの行を加えて全ての列からちょうど1回ずつ選ぶことにする。
これでよく知られた割り当て問題になるっぽい。
こんな質問に東工大…全力で答えてくれました。
ちなみに調べてみると、東工大OCWは、東工大が、すべての講義資料を全世界に向けて無償で公開しているプラットフォームなんだとか…
なんだかよくわからない凄そうな講義資料がずらずらと並んでいます。
ということで、ハンガリー法を少しググってみると、なるほど。
世間的は、こんな時に提起される問題を割当問題と言うのだそうです。
(例題)
4人の作業員と4つの仕事がある。
それぞれの作業員がそれぞれの作業を行うのに求める給与は以下の表の通り。
総コストを最も低くする割当方法は?
| 作業W | 作業X | 作業Y | 作業Z | |
| Aさん | 3 | 2 | 1 | 3 |
| Bさん | 4 | 3 | 1 | 2 |
| Cさん | 4 | 2 | 4 | 5 |
| Dさん | 2 | 4 | 3 | 1 |
この様な問題を解く際、上記の様な数であればなんとなくで解くことも出来ますが、これが10人×10作業ぐらいになったあたりから難易度は飛躍的に上がります。
そこで、なんとなくではなく、しっかりとした解放としてハンガリー法(ハンガリアン法)というものが提案されているのだそうです。
ハンガリー法とは
ハンガリー法には主に4つのステップがあります。
SETP1 各行各列に0を作る。
まずは各行で0を作ります。
各行ごとに、最小値を見つけ、それぞれの値からその最小値を引きます。
最小値はA,B,C,Dの順に、1,1,2,1なので、それぞれ行から引いた結果がこちら。
| W | X | Y | Z | |
| A | 2 | 1 | 0 | 3 |
| B | 3 | 2 | 0 | 1 |
| C | 2 | 0 | 2 | 3 |
| D | 1 | 3 | 2 | 0 |
各列でも同様の処理を行います。
列W以外は0が存在するので、何も変わりませんね。
| W | X | Y | Z | |
| A | 1 | 1 | 0 | 3 |
| B | 2 | 2 | 0 | 1 |
| C | 1 | 0 | 2 | 3 |
| D | 0 | 3 | 2 | 0 |
STEP2 適切な割り当てがあるかどうか、検討する
この状態で、各行各列で重複が無いように選択することが出来れば、それが回答です。
多くの場合、今回の例と同様、この段階で適切に選択することが出来ません。
その場合にはSTEP3に進みます。
STEP3 出来るだけ少ない本数の線で0を消す
この辺りから少しパズルの様なことを行っていきます。
以下の用に、出来るだけ少ない本数の線で0を消します。
(今回は線ではなく、黒塗りで表現しました)
| W | X | Y | Z | |
| A | 2 | 1 | 3 | 0 |
| B | 3 | 2 | 0 | 1 |
| C | 2 | 0 | 2 | 3 |
| D | 1 | 3 | 2 | 0 |
STEP4 新たな表を作り、SETP2に戻る
線で消されていない(黒塗りになっていない)数字に注目します。
この中で最小値をみつけ、それぞれの値からその最小値を引きます。
黒塗りになってる部分はいじりません。
最小値、今回の例の場合は1ですね。
| W | X | Y | Z | |
| A | 1 | 0 | 2 | 0 |
| B | 3 | 2 | 0 | 1 |
| C | 2 | 0 | 2 | 3 |
| D | 0 | 2 | 1 | 0 |
次に、線が交差する部分(今回の様に塗るとわかりづらいですが、線で想像してみてください)に、先ほどの最小値を足します。
以下の表でオレンジ色の部分ですね。
| W | X | Y | Z | |
| A | 1 | 0 | 2 | 0 |
| B | 3 | 2 | 0 | 2 |
| C | 2 | 0 | 2 | 4 |
| D | 0 | 2 | 1 | 0 |
STEP2-2
| W | X | Y | Z | |
| A | 1 | 0 | 2 | 0 |
| B | 3 | 2 | 0 | 2 |
| C | 2 | 0 | 2 | 4 |
| D | 0 | 2 | 1 | 0 |
赤く塗った部分を選べば、各行各列で重複なく選択することが出来ますね。
つまり
A:Z B:Y C:X D:W
が回答となります。
尚、回答がひとつとは限らず、複数の回答が出てくる可能性もあります。
これでも回答が出ない場合には、再びSTEP3、STEP4、STEP2、STEP3、STEP4と回答が出るまで同じことを行うと、必ず最終的には答えが出ます。
また、STEP2に関しては線の引き方が複数ありますが、その引き方によって、何回目のSTEP2で答えが出るかが変化することも。
それでも、必ず答えが出るのだそうです。
本当にこれが答えなのか、どれだけ多くの数でやっても答えが出るのか。
ちょっと半信半疑になってしまいますが、数学的にきっちり証明されているんだそうですよ!
同じものを複数選択できる用に拡張する
ようやく光が見えてきました。
ただしこのハンガリー法、これまで見て来た例の様に、行と列の数が揃っている場合(正方行列)でしか使うことが出来ません。
そこで、A君からのアドバイス
ただし、今の問題をちょっと変形する必要があって
- 列の中から複数回選ぶ代わりに、同じ列を加えて、1つの列から1回しか選べないことにする。
- さらに全ての成分が0となるようなダミーの行を加えて全ての列からちょうど1回ずつ選ぶことにする。
これでよく知られた割り当て問題になるっぽい。
これが効いてくるんですね。
僕がfacebookで提示した例で考えてみましょう。
| A | B | C | D | |
| ① | 1 | 2 | 4 | 5 |
| ② | 3 | 1 | 2 | 4 |
| ③ | 1 | 3 | 5 | 7 |
| ④ | 4 | 2 | 1 | 3 |
| ⑤ | 7 | 5 | 4 | 2 |
※選択可能回数:A-1回 B-1回 C-2回 D-3回
この行列をA君の言うとおりに拡張してみます。
| A | B | C | D | C | D | D | |
| ① | 1 | 2 | 3 | 4 | 3 | 4 | 4 |
| ② | 3 | 1 | 2 | 4 | 2 | 4 | 4 |
| ③ | 1 | 3 | 5 | 7 | 5 | 7 | 7 |
| ④ | 4 | 2 | 1 | 3 | 1 | 3 | 3 |
| ⑤ | 7 | 5 | 4 | 2 | 4 | 2 | 2 |
| ⑥ | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⑦ | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
まずはSETP1。
| A | B | C | D | C | D | D | |
| ① | 0 | 1 | 2 | 3 | 2 | 3 | 3 |
| ② | 2 | 0 | 1 | 3 | 1 | 3 | 3 |
| ③ | 0 | 2 | 4 | 6 | 4 | 6 | 6 |
| ④ | 3 | 1 | 0 | 2 | 0 | 2 | 2 |
| ⑤ | 5 | 3 | 3 | 0 | 2 | 0 | 0 |
| ⑥ | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⑦ | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
列変換に関しては、⑥、⑦に全てが0のダミー値を入れているため、最初は必ず何もしないことになります。
次にSTEP2ですが、①と③で0の出現の仕方が全く同じであるため、いきなり適切な選択は出来ません。
ということでSTEP3。
| A | B | C | D | C | D | D | |
| ① | 0 | 1 | 2 | 3 | 2 | 3 | 3 |
| ② | 2 | 0 | 1 | 3 | 1 | 3 | 3 |
| ③ | 0 | 2 | 4 | 6 | 4 | 6 | 6 |
| ④ | 3 | 1 | 0 | 2 | 0 | 2 | 2 |
| ⑤ | 5 | 3 | 3 | 0 | 2 | 0 | 0 |
| ⑥ | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⑦ | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
STEP4。
| A | B | C | D | C | D | D | |
| ① | 0 | 1 | 1 | 2 | 1 | 2 | 2 |
| ② | 2 | 0 | 0 | 2 | 0 | 2 | 2 |
| ③ | 0 | 2 | 3 | 5 | 3 | 5 | 5 |
| ④ | 4 | 2 | 0 | 2 | 0 | 2 | 2 |
| ⑤ | 6 | 4 | 3 | 0 | 2 | 0 | 0 |
| ⑥ | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| ⑦ | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
まだ①と③が同じ形、ダメですね…
もう1度STEP3、STEP4です。
| A | B | C | D | C | D | D | |
| ① | 0 | 1 | 1 | 2 | 1 | 2 | 2 |
| ② | 2 | 0 | 0 | 2 | 0 | 2 | 2 |
| ③ | 0 | 2 | 3 | 5 | 3 | 5 | 5 |
| ④ | 4 | 2 | 0 | 2 | 0 | 2 | 2 |
| ⑤ | 6 | 4 | 3 | 0 | 2 | 0 | 0 |
| ⑥ | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| ⑦ | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| A | B | C | D | C | D | D | |
| ① | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| ② | 3 | 0 | 0 | 2 | 0 | 2 | 2 |
| ③ | 0 | 1 | 2 | 4 | 2 | 4 | 4 |
| ④ | 5 | 2 | 0 | 2 | 0 | 2 | 2 |
| ⑤ | 7 | 4 | 3 | 0 | 2 | 0 | 0 |
| ⑥ | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| ⑦ | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| A | B | C | D | C | D | D | |
| ① | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| ② | 3 | 0 | 0 | 2 | 0 | 2 | 2 |
| ③ | 0 | 1 | 2 | 4 | 2 | 4 | 4 |
| ④ | 5 | 2 | 0 | 2 | 0 | 2 | 2 |
| ⑤ | 7 | 4 | 3 | 0 | 2 | 0 | 0 |
| ⑥ | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| ⑦ | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
できました!!!
ということで今回の回答は
①:B ②:C ③:A ④:C ⑤:D
で、なんとなくで判断した結果と一致しています。
実装する
本当はここからが大変でした…
考え始めてのべ4日、期間としては1週間、ハンガリーを知ってからコードに落とし込むまで丸2日。
Google Apps Scriptとして実装しました。
10人に12個のBCから適切な物を配布する計算を何度か実行してみましたが、計算に要した時間は0.5秒~1.7秒。
ハンガリー法を手作業でやっていたら数分~十数分は最低でもかかるのでは無いかと思います。
もしかするともっとかかるかも…
さらに、なんとなくで考えていたら何時間かかることやら…
これで、似通った体系の人がやけに多い日も安心ですね!(笑)
いつになく一見ダイビングとは関係無い様な内容になってしまいましたが、レンタル器材の配布にお困りの方は、是非お声がけください(笑)
付録
書く人が書けば、もっとすっきりかけるのかも知れませんが、今の僕が書くとこんな感じです。
function hungarian(ary,stock,name){
var member = ary.length;
for(var i=0;i<name.length;i++){
for(var j=0;j<stock[i]-1;j++){
for(var k=0;k<member;k++){
ary[k].push(ary[k][i]);
var addname = name[i];
}
name.push(addname);
}
}
//add row
var lackrow = ary[0].length - ary.length;
if(lackrow > 0){
for(var i=0;i<lackrow;i++){
var addrow = [];
for(var j=0;j<ary[0].length;j++){
addrow.push(0);
}
ary.push(addrow);
}
}
for(var i=0;i<ary.length;i++){
var rowmin = ary[i][ary[i].indexOf(Math.min.apply(null,ary[i]))];
for(var j=0;j<ary[i].length;j++){
ary[i][j] = ary[i][j] - rowmin;
}
}
for(var i=0;i<ary.length;i++){
var col =[];
for(var j=0;j<ary.length;j++){
col.push(ary[j][i]);
}
var colmin = ary[col.indexOf(Math.min.apply(null,col))][i];
for(var j=0;j<ary.length;j++){
ary[j][i] = ary[j][i] - colmin;
}
}
var res = [];
while(res.length==0){
var copyary = [];
for(var i=0;i<ary.length;i++){
var copyrow = ary[i].slice();
copyary.push(copyrow);
}
res = search(copyary);
if(res.length>0){
for(var i=0;i<res.length;i++){
res[i][1] = name[res[i][1]];
}
return res;
break;
}
var ary = makenewary(ary);
}
}
function cntrowzero(ary){
var rowzero = [];
for(var i=0;i<ary.length;i++){
var cntzero = 0;
for(var j=0;j<ary[0].length;j++){
if(ary[i][j]==0){
cntzero++;
}
}
rowzero.push(cntzero);
}
return rowzero;
}
function cntcolzero(ary){
var colzero = []
for(var i=0;i<ary[0].length;i++){
var cntzero = 0;
for(var j =0;j<ary.length;j++){
if(ary[j][i]==0){
cntzero++;
}
}
colzero.push(cntzero);
}
return colzero;
}
function makenewary(ary){
var rowzero = cntrowzero(ary);
var colzero = cntcolzero(ary);
var copyary = [];
for(var i=0;i<ary.length;i++){
var copyrow = ary[i].slice();
copyary.push(copyrow);
}
var rowline = [];
var colline = [];
for(var i=0;i<ary.length;i++){
rowline.push(i);
}
for(var i=0;i<ary[0].length;i++){
colline.push(i);
}
var rowzeromax = rowzero[rowzero.indexOf(Math.max.apply(null,rowzero))];
var colzeromax = colzero[colzero.indexOf(Math.max.apply(null,colzero))];
var maxsum = rowzeromax + colzeromax;
var p = 0;
for(var i=0;maxsum>0;i++){
if(rowzeromax > colzeromax){
p = 0;
}else if(rowzeromax < colzeromax){
p = 1;
}else{
if(p==1){
p=0;
}else{
p=1
}
}
if(p==0){
copyary.splice(rowzero.indexOf(Math.max.apply(null,rowzero)), 1);
rowline.splice(rowzero.indexOf(Math.max.apply(null,rowzero)), 1);
rowzero.splice(rowzero.indexOf(Math.max.apply(null,rowzero)), 1);
colzero = cntcolzero(copyary);
}else{
for(var j=0;j<copyary.length;j++){
copyary[j].splice(colzero.indexOf(Math.max.apply(null,colzero)), 1);
}
colline.splice(colzero.indexOf(Math.max.apply(null,colzero)), 1);
colzero.splice(colzero.indexOf(Math.max.apply(null,colzero)), 1);
rowzero = cntrowzero(copyary);
}
rowzeromax = rowzero[rowzero.indexOf(Math.max.apply(null,rowzero))];
colzeromax = colzero[colzero.indexOf(Math.max.apply(null,colzero))];
maxsum = rowzeromax + colzeromax;
}
var minary = [];
for(var i=0;i<copyary.length;i++){
minary.push(copyary[i][copyary[i].indexOf(Math.min.apply(null,copyary[i]))]);
}
var min = minary[minary.indexOf(Math.min.apply(null,minary))];
for(var i=0;i<rowline.length;i++){
for(var j=0;j<colline.length;j++){
ary[rowline[i]][colline[j]] = ary[rowline[i]][colline[j]] - min;
}
}
for(var i=0;i<ary.length;i++){
for(var j=0;j<ary[0].length;j++){
if(rowline.indexOf(i)==-1 && colline.indexOf(j)==-1){
ary[i][j] = ary[i][j] + min;
}
}
}
return ary;
}
function search(ary){
var res = [];
var row = [];
var col = [];
for(var i=0;i<ary.length;i++){
row.push(i);
col.push(i);
}
for(var i=1;i<ary[0].length+1;i++){
for(var j=0;j<ary.length;j++){
var zero = ary[j].indexOf(0);
var cnt=0;
for(var k=0;k<ary[j].length;k++){
if(ary[j][k]==0){
cnt++;
}
}
if(zero == 0 && cnt <= i){
ary.splice(j,1);
if(ary.length == 0){
res.push([row[j],col[0]]);
break;
}
for(var k=0;k<ary[0].length;k++){
ary[k].splice(0,1);
}
res.push([row[j],col[0]]);
row.splice(j,1);
col.splice(0,1);
j=-1;
i=0;
}
}
if(ary.length == 0){
break;
}
}
if(ary.length > 0){
res = [];
}
return res;
}
